■ ACMT/ 劉文斌
噴泉流動(FountainFlow)
塑膠材料和金屬材料最大的性質差異，可以由材料的應變( 變形量值) 和材料模數(modulus- 楊氏模數，彈性模數) 之間的變化關係來區別。塑膠材料的應力- 應變參數的變化性質是在產品設計上重要的參考依據。
圖1。顯示為金屬材料典型的應力- 應變曲線圖，在此曲線上包含著一段線性比例關係的區域，此區域的材料行為符合所謂的虎克定律(Hook’sLaw) 彈性行為。此彈性區域的材料模數( 楊氏模數，彈性模數) 為一常數定值；所謂模數Modulus=(stress)/(strain) 即為應力-應變曲線上的對應斜率，在此彈性區域上可以藉由簡單的應變數值與起始彈性模數的乘積，來計算出應力值，可作為產品設計上的參考依據。
另外，如下圖2。則顯示塑膠材料典型的應力- 應變曲線圖，由圖型中可知塑膠材料的彈性區域- 或線性比例區域，只存在於起始原點附近非常小的區域內，整體的應力- 應變曲線則呈現較大的圓弧形狀，而且模數( 曲線的斜率) 會隨著應變的量值變化而逐漸改變，所以塑膠的材料特性是會表現應變是模數的函數，模數將會隨應變量不同而變化不同( 不是一個定值)。所以塑膠材料和金屬材料不同，塑膠材料的破壞應力值將會小於起始彈性模數與應變的乘積值。
針對塑膠材料的設計考量上，並不能像金屬一樣直接使用彈性模數與變形量的乘積來作為破壞應力的設計，塑膠材料的使用範圍是在較大應變量區域，因為已經超出線性比例的彈性範圍外，所以在產品破壞應力設計上，需要考慮在起始比例線性彈性模數範圍外的應力- 應變關係。如下圖3。所示在塑膠的應力-應變曲線圖型上，根據適當的應變量作一割線(Secant ine)，並求得此割線的彈性模數值( 斜率值)-(Secant odulus) 來作為設計上的參考依據。換言之，要以彈性模數隨應變變形量的變化情況來進行塑膠產品破壞應力值的設計。
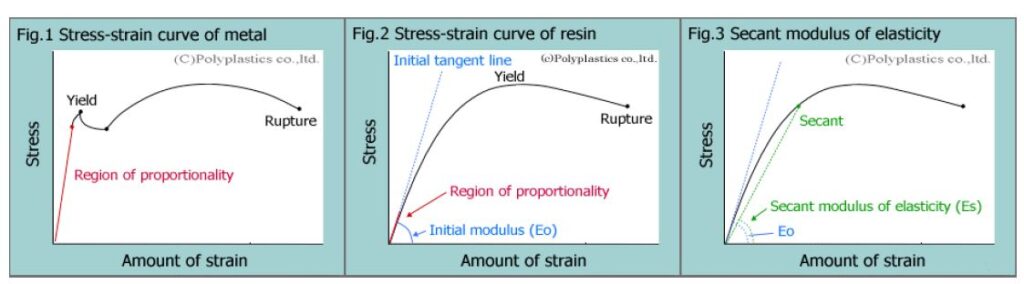圖1: 金屬材料的應力- 應變曲線圖/ 圖2: 塑膠材料的應力- 應變曲線圖/ 圖3: 塑膠材料的割線彈性模數
外觀彈性模數對應變的依存性(Dependence of apparent modulus of lasticity on strain)
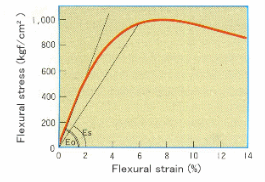
依照塑膠的特性，在塑膠材料的應力- 應變曲線上，幾乎會找不到應力隨應變呈比例關係而符合虎克定律的彈性變形區域；由塑膠的應力- 應變圖形上( 如下圖)可以觀察到塑膠材料的彈性模數會隨不同應變量而變化，從圖形上可知對應到不同應變量( 或應力值) 的彈性模數，可以藉由圖形上對應的點與原點來作一割性，此割線的斜率即為該應變值的彈性模數又稱為正割彈性模數(Secant Modulus of Elasticity,Es)。所以針對塑膠材料當進行較精準的設計時，建議不要直接拿材料型錄或物性表上初始彈性模數-Eo 來作設計，而需要使用正割彈性模數-Es 來替代。
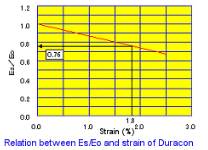
例如Polyplastics 的CopolymerPOM_Durcon 材料，其正割彈性模數-Es 與初始彈性模數-Eo 的比值和應變值作圖如下圖所示。當應變量小於2% 時，圖形關係並不會受到應力負荷的延遲( 經過時間) 與溫度的影響，且從過去的經驗得知，這種在低應變量區域的Es/Eo 關係也並不會受到塑料的種類或是等級料不同所影響。
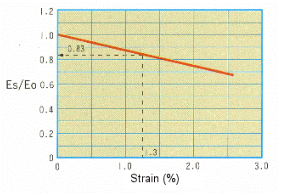
使用Es/Eo 的計算範例(Examples of calculation by using Es/Eo)
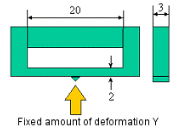
現有一簡易固定梁如下圖所示，要計算在樑柱中央位置產生一0。3mm 變形量時，所頓應的破壞應力值； 簡易梁所使用德材料為Polyplastics 的CopolymerPOM_DurconM90-44 等級，環境溫度為23C。計算方法及設計時的應力荷重修正如下：
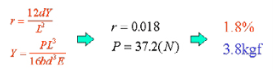
彈性模數(E) 的修正-Correction of modulus of elasticity (E) X Es/Eo =2580X0.76 = 1960使用此修正過的E 值帶入上面算式計算，可得：P= 2.9 Kgf■
