■耀德講堂/ 邱耀弘 博士
前言
經前二期介紹後,相信讀者們對金屬粉末已有初步了解,然而我們要更清楚的是有關粉體的兩個特徵:「粉體的尺寸」與「表面形狀」,關於巨觀(Macroscopic)、介觀(Mesoscopic) 與微觀(Microscopic) 的尺度理解,讓Dr.Q 來為大家科普一下!
• 巨觀(或稱宏觀)尺寸:>1mm
• 介觀尺寸:1mm< 尺寸<1μm
• 微觀尺寸:<1μm 所以巨觀> 介觀> 微觀,在科學上的尺寸定義非常明確,那麼有趣的是:金屬粉末射出成型或是金屬增材製造的尺度範圍將橫跨上述三觀,能清楚地描述將微米級粉末(微觀)聚集成喂料(介觀結構),再經過射出成型成為巨觀/ 介觀的實體成品之三觀變化(如圖1 所示)。
因為粉末是固態物質,卻同時具有三個相(Samestate with three phases,同態三相),且又橫跨三觀(微/ 介/ 巨,Micro-/Meso-/Macroscopic)的奇妙物理狀態。人們自老祖宗就與粉末為伍,卻又渾然不知(如泥土、麵粉等),本文將探討金屬粉末形狀之影響。
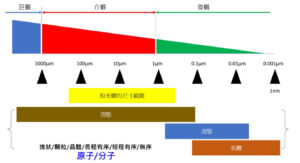
圖1:物質的表現包含三觀、三態,是以尺寸做為區分的參考標準
粉末的尺寸
當讀者們理解了尺度的三觀後,我們利用圖2 來實際解釋有關尺度的差異,三個顏色的方塊的總和體積是相同的,B 方塊是將A 方塊從邊長(X / Y / Z) 分別等分為2;C 方塊則以A 方塊從邊長(X / Y / Z) 等分成4。那麼粒子的尺寸基本影響就可以單由表面積來解釋,面積的計算分別如下:
• A 方塊總表面積10 X 10 X 6(面) X 1 (個)= 600 (μm2)
• B 方塊群的總表面積(10 / 2) X (10 / 2) X 6(面)X 8 (個)= 1200 (μm2)
• C 方塊群的總表面積(10 / 4) X (10 / 4) X 6(面)X 16 (個)= 2400(μm2)
以更直觀的案例來說明,當老闆派發工作,如果給三種顏色的油漆刷A / B / C 三個方塊,且油漆只要塗一層(一樣厚度),則消耗油漆的總量是A < B < C;而如果A / B / C 都各發一桶相同容積的油漆且要全部用完,刷完所有方塊後,則油漆層的厚度為A > B > C。這樣讀者就可以了解當粒子或是粉末在相同重量(或體積)下,尺寸大小對於物理性質上的實質影響──相同重量(或體積)下,尺寸變小,則表面積增大。
再來計算尺寸造成顆粒數量和表面積增量的明顯數據,使用標準密度為7.9g/cc 的不鏽鋼316L 球形粉末,假設粉末都是單一直徑,那麼1g 重的不鏽鋼316L 粉末總數量和表面積大小條列如圖3,這是Dr.Q 在許多公開場合的講義教材中最常拿來說明的案例。
粉末的形狀
另一個基本物理描述是沒有辦法用單一數學公式描述的,就是幾何形狀。儘管科學家能夠用更為精確的辦法來測量,但就像自然界的3 大奇數(奇怪且奧妙):e(指數)、π(圓周率)、i(虛數),相信學過工程數學或是微積分的人都知道三角函數就是這三大奇數的組合,這邊Dr.Q 還是先跳過!(Dr.Q 答應大家在接下來內文中工程上的數學只談加、減、乘、除和開三次根號!)
平常為方便數學計算,實際上皆以圓球來做為粉末的基本計算,然而隨計算速度和電腦記憶體容量的提升,更接近實體模擬的計算也逐漸地進行,如圖4 中作為粉末近似的模擬幾何形狀,不過,這些的模型都是以等軸粉體(Equiaxed) 進行模擬,還不能真正代表實際的粉體形狀。(等軸粉體,即是任意取直線由任意表面通過本體的質量或形體中心到另一表面,將隨機取得的這類型數道直線長度做加總平均,所得到的數據幾乎都是相等的。)
因此,聰明的人類祖先想到的辦法就是限度樣品(Limitation Sample) 比對法,如圖5 所示。這些數值化的計算到現在還在努力地進行中,因為實際粉末的數量實在是一個無窮大的數字,且尺寸分布還不是均勻的,這也是微觀世界最有趣且大而化之的科學,將量子力學的測不準理論(Uncertainty principle) 用於解釋粉體的平均特性,是真的可以符合的。
細粉的可能危害
說到這也差不多是時候結束本次粉體科學議題了,相信粉末製程的同業們一定都領教過細粉帶來的痛苦和教訓,重量級別可能不到1% 的細粉卻導致製程失敗,甚至發生危險,尤其是奈米級粉末的高比表面積,往往會在製程中形成觸媒效應,1% 不到的粉體在顆粒數量巨大甚至超過其餘99% 的粗大粉體,因為細粉增加的表面積,使得粉體之間的摩擦力大幅增加。
此外,小於介觀尺寸以下時,要留意到因為重力的影響變小,細微粉末展現出同態三相中最危險的氣相飛揚,這也是粉體製品業者要留心的,尤其是粉塵造成的危害(如劇烈氧化、吸入人體等);無機材料的細長比(Slender ratio, L / D,其中L 為纖維長度,D 為纖維直徑),當纖維直徑非常細小時(小於5μm),且L / D > 5 時,就非常危險,操作人員須謹慎行事。
結論
對於基本粉末科學和金屬粉末的認知,經過Dr.Q 幾篇的分析和討論,不知道大家是否對於它們有更深地了解呢?套一句哲學的科學結論,當物質的「顆粒尺寸愈小,它們相互糾纏的距離便可以愈遠」,大家覺得有沒有道理呢?引用量子糾纏(QuantumEntanglement) 這個名詞,它是量子粒子之間的連接,是宇宙的基本結構單元。一旦兩個粒子發生糾纏,當一個粒子發生變化,便會立即在另一個粒子中反映出來,不管它們是在同一間實驗室,還是相距數億光年。
很有趣對吧!當物質聚集成愈大的粒子時,就具有明顯的質量增加效應,那麼也就只能和愈接近的粒子互相糾纏,畢竟能夠相互輝映的粒子們就在身邊,但是當粉末的尺寸愈變愈小,且距離愈來愈遠的時候,量子糾纏的行為就明顯起來,這樣的哲學推論在近代物理學已經被證實,無怪乎哲學是凌駕科學之上。雖然粉末的尺寸比起量子尺寸要大上幾十個冪次(μm / 量子尺寸 >10 的10 次方),我們在微觀與介觀過程中進行製造,所得到的巨觀結果產品,這是一種利用微米級粒子糾纏的原理,已經被現代粉末技術(粉末壓製 / 粉末射出成型 / 粉末增材製造)所靈活應用。
各位讀者,唯有以科學加以證實的理論,並加以應用,我們才能真正理解「上帝的粒子」之奧妙。有一天,我們都將成為上帝粒子的一部分,但其實這些粒子早已存在於我們身體中,當你在閱讀本文時,便早已經構成了Dr.Q 與ACMT 對你身體中的粒子進行相互的糾纏了!■
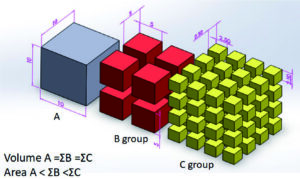
圖2:三個顏色的正立方體均質方塊,尺寸單位假設為μm
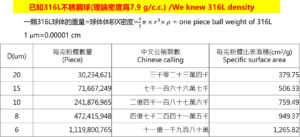
圖3:每1g 不鏽鋼316L 球形粉末的數量與表面積對應(D 為直徑)
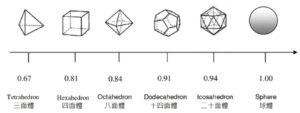
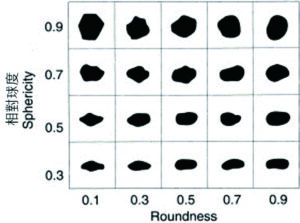
圖4:類似於現有元素分析的作法,把粉末歸類於幾個模型以便進行高階演算
圖5:用於粉末科學的相對球度比較法樣本




