■ Moldex3D
摘要
塑膠光學元件已經被廣泛的應用于各種工業界應用, 如鏡頭、燈罩、光碟、光導板等。然而，透明性塑膠射出元件的雙折射問題嚴重地影響著光學成像品質，已經被視為重要的產品品質指標。雙折射在射出制程中主要由材料流動受到的剪切效應與溫度凍結所影響。本文以一個整合式的數值模擬方法將射出成型制程中各階段因素在計算中加入考慮，並成功的預測出雙折射分佈。模擬結果與實驗比對有相當之吻合，驗證本研究所提出之模擬方法是可信賴的模擬工具。
關鍵字：雙折射、光學、射出成型
1.前言
隨著塑膠工業的不斷發展，光學塑膠的材料特性逐日提升，而制程的技術也持續在進步，越來越多射出成型之光學產品已經被運用到各種光學應用產業，如光電產業常見的光學鏡頭與導光板等。
射出的光學元件，主要有收縮變形與雙折射等問題，收縮變形目前可透過制程參數的調配與模具補償加以改善，作用原理與模擬預測均被大家所廣為熟悉。但是雙折射問題影響整體光學系統之光程差，對成像品質造成不良的影響，實務上不容易做像差矯正，且在模擬預測的發展上較為緩慢，尚未發展出成熟與可信賴的模擬工具供業界參考。
雙折射是光線穿透過透明性材料時，分解為兩道有快慢差異之光線。光線速度快慢的不同與經過厚度方向的累計後，會產生光路程相位上的落差，稱之為光程差。當以偏振光觀察雙折射晶體材料時，由各光線亮度上的相互消長，產生明暗相間的光彈條紋，而其條紋級數與材料內部之主軸應力差值成正比，代表著材料受力之狀況。雙折射現主要成因是由高分子的光學非等向所導致，微觀下的高分子在軸向、背脊或側鏈方向的光學偏振特性不同，因此空間上之分子排向不一致，雙折射之程度也就不同。以現在光學元件逐漸輕薄短小之趨勢下，在狹小的流動空間下，流動導致之非等向性將非常嚴重，因而流動導致之雙折射預期將成為光學元件在以射出成型製造上的主要技術瓶頸。
本文之類比方法是建立在三維實體的流動分析過程，以黏彈性分析所預測出的流動殘餘應力為出發，對於三度空間中的非等向性的分子排向而產生的雙折射現象能有良好的掌握。再整合以體積收縮與冷卻均勻性為考量的熱應力分析，將光學非等向性質區分為流動影響與熱影響兩部分。此整合式之模擬工具希望在未來應用上，可以協助提供各影響光學性質的重要因數之詳細資訊，如幾何外型、澆口設計、射速、保壓、冷卻系統等。
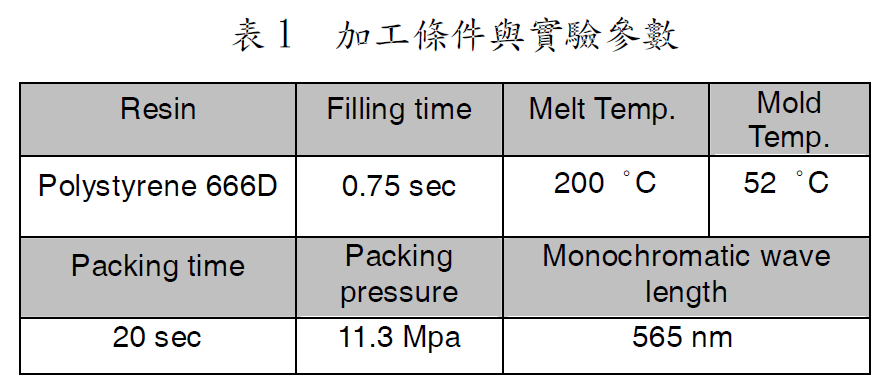表1：加工條件與實驗參數
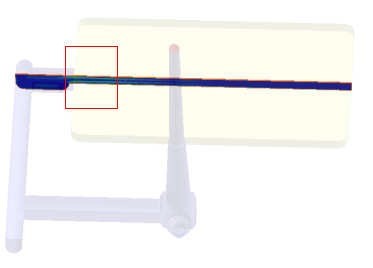
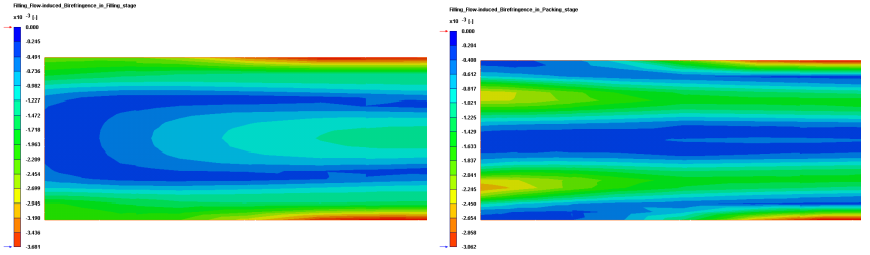
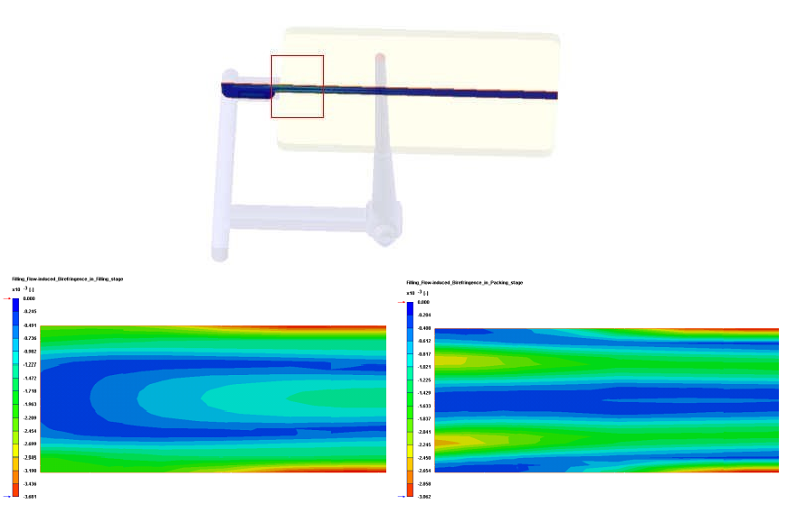
圖1: 模擬之雙折射分佈於靠近澆口之厚度方向切面 (a) 平板案例之幾何外型與切面位置,(b) 流動結束 時之雙折射分佈,(c) 保壓結束時雙折射之分佈
2.數值模型
假設高分子熔膠行為為黏彈性流體，非恒溫的三維流動之數學方程式可以表示如下：
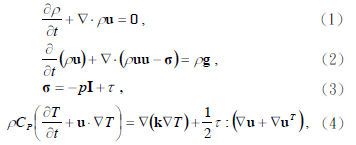
其中，u 為速度向量、T 為溫度、t 為時間、 p 為壓力、σ 為總應力張量、ρ 為密度、τ 為額外應力張量、k 為熱傳導係數、C 為比熱。在本文中，τ 由White-Metzner 模型的本質方程式可得：
其中，λ 為鬆弛時間而η 為黏度，兩者皆式溫度與剪切率的函數。
體積分率函數 f ，用來追蹤波前的移動。f = 0 代表為空氣， f = 1 為高分子熔膠，而波前的位置就是落在格點中體積分率為0 < f < 1 的區域。體積分率隨著時間的推進可以表示為下列的傳輸方程式：
在模穴入口處之進膠面給定充填流率或者射出壓力，在模壁給定無滑移邊界條件，而特別需要注意的是，在體積分率的傳輸方程式中，由於是雙曲線式之方程式，只需給定入口邊界條件。
本文，利用有限體積法(Finite Volume Method ) 求解各流場與應力相關之統馭方程式，而數值核心在文獻
[5] 已經被驗證可以成功的應用在射出成型充填模擬，許多實驗與測試也確認了此數值核心在可靠度上與效率上的表現。 雙折射大小與塑膠內部所承受主軸應力差值的成正比，此現象為所謂之光學應力定律，如下：
其中，n1 與n 為主軸方向之折射率，σ 與σ 為主軸應力，而C 為光學應力常數。
在光線穿過雙折射晶體，由快慢兩光線而形成相位的差異，若以長度表示，一般稱之為光程差。光程差與雙折射大小及材料厚度成正比：δ = Δnd . (8)
條紋級數 N ，則定義為光程差與光波長λ 之比值，可表示如下：
圖2：光彈分析(a) 預測之流動導致光彈條紋,(b) 預測之熱導致光彈條紋,(c) 成品總光彈條紋, (d) 成品條紋級數,(e)實驗觀察之光彈條紋[6]
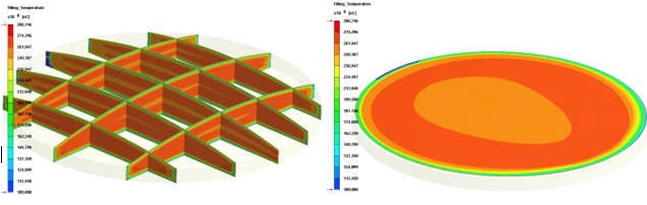
圖3：凸透鏡模型(a) 波前分佈,(b) 不同方向切面上之溫度分佈
3.結果與討論
本文首先採用一Lehigh U.[6] 所用之長方形薄板，作為與實驗比對之案例。幾何外觀分別為3.3 mm (厚度)x 101.6 mm ( 長度) x 50.8 mm ( 寬度)。材料選定為PS Styron 666D，料溫與模溫分別設定為200 ℃ and 52℃，充填時間為0.75 秒，保壓時間則為20 秒。相關材料與加工條件之資訊整理如表1 。而此案例之網格，為厚度方向上有20 層的混合三維元素。圖1(a) 至(c) 為模擬出之雙折射於厚度方向切面上之分佈，在流動結束時( 圖2(b))，雙折射分佈之最高值出現於靠近模壁之表面，這主要由在充填過程中，模壁表面受到模壁低溫影響而快速冷卻使得流動應力與分子排向凍結所導致。而中心部份有相對較弱的分佈，由此切面是靠近澆口，熔膠承受幾何形狀上之收縮，而厚度方向上有速度及其伴隨之應力，此細部現象只能由三維之模擬所掌握。在保壓結束時( 圖2(c))，由於表面分子排向已經被凍結，但是中心高溫之熔膠仍然受到額外塑膠流進的影響，在中心處形成額外的波峰，形成局部高值，此結果與文獻[1,2,4] 之觀察有吻合之結果。
圖2 (a) 至(c) 為光彈分析之結果，圖2(a) 為流動導致之光學常數為 動導致光彈條紋，其分佈與波前的分佈接近，且於靠近澆口的區域較為密集。
圖2(b) 為熱導致之光學常數 下，數值預測之熱導致之光彈條紋，其分佈接近同心圓的型狀，其成因主要為內部高溫之熔膠冷卻至室溫所伴隨的非均勻收縮所造成。由於PS 材料熱導致之雙折射相對於流動導致之雙折射小，因而熱導致之光彈條紋較不明顯，但是PS 材料的光學應力常數在玻璃轉換溫度前後，光學應力常數有正負號不同，因而在成品總光彈條紋會呈現部分補償作用，預測之光彈條紋如圖2(c)，而圖2(d) 則為總光彈條文級數。將圖2(c) 與(d)與實驗結果圖2(e) 相比較，可以發現大部分之特徵均有吻合，而細部區域之不同可能為目前科學理論對於光學常數的掌握之不足與黏彈性計算分析上有其他更正確卻複雜之模型有待引入，然而目前之三維模擬結果已有相當之吻合，計算效率與穩定度預期足以符合之工業之需求。
本文並再以凸透鏡案例進行模擬，進一步展示目前的類比方法的對於光學產品的適用性。其半徑與厚度分別為36 mm 與4 mm，材料為Zeonex 480R，料溫設定為270 ° C，模溫設定為100 ° C，充填時間0.3 秒，保壓時間10 秒，保壓壓力60 Mpa。文獻[7] 指出COP 材料所產生的雙折射主要受到流動效應影響為主，受熱效應影響較小，因而本文在探討此凸透鏡案例時，主要在討論流動相關的波前、溫度、剪切率、流動殘餘應力與流動導致雙折射等。 圖3 (a)為凸透鏡案例之波前分佈，由於凸透鏡之幾何形狀配合側面中心進膠，流動末端為最遠離澆口之區域，沒有產生凹透鏡常見之包封現象。圖3 (b) 為不同切面上之溫度分佈，表面溫度最低，而在靠近表面之處則有剪切生熱所產生之溫度升高現象。圖4 (a) 為流動結束時之剪切率分佈，剪切率呈現靠近澆口最大，而在末端由於幾何形狀之壓縮而再度升高。圖4 (b) 為流動應力分佈，主要是受到流場變化的剪切效應與溫度分佈所呈現的凍結（鬆弛）效影所影響。圖4 (c)為流動應力之最大主軸應力，其代表高分子在剪切流動階段受到最大拉伸應力，由其方向與大小可以分別看出高分子的排向與排向的強度。由流動應力及其分子排向，配合光學應力定律，可以得到流動導致雙折射，如圖4 (d)。以上結果吻合文獻[7] 所得到的實驗觀察與其結論。
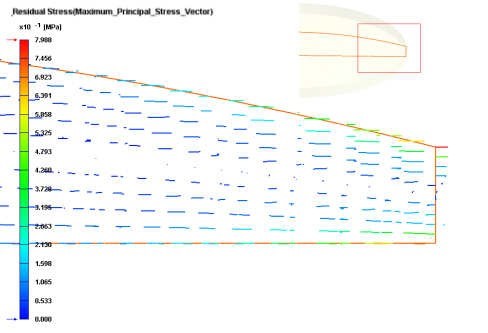
圖4 (a) 流動階段之剪切率分佈, (b) 流動殘餘應力, (c) 最大主軸流動應力, (d) 流動導致之雙折射
4.結論
本文所使用之數值方法建立在三維實體的流動分析，配合黏彈性分析所預測出的流動殘餘應力，對於三度空間中的非等向性的分子排向而產生的雙折射現象能有良好的掌握。並再整合以體積收縮與冷卻均勻性為考量的熱應力分析，區分雙折射為流動影響與熱影響兩部分，可以從結果思考如何修改加工參數、澆口設計等影響光學性質的重要因數。 本文之結果除了可模擬出射出各階段下的流動導致之雙折射與受熱應力導致之雙折射，並進一步整合光彈分析理論，提供在光線穿過物體後所累積之光程差、條紋級數與光彈條紋等實用資訊，做到與實務緊密結合，提供方便易判讀結果之模擬工具。
- 參考文獻
1.Y. B. Lee, T. H. Kwon, and K. Yoon, Polymer Engineering and Science, 2002, 42:2246.
2.A. I. Isayev, G. D. Shyu, and C. T. Li, J Polym SciPoly Phys, 2006, 44, 622.
3.G. D. Shyu, A. I. Isayev, C. T. Li, J Polym Sci Poly Phys 2001, 39, 2252.
4.R. Pantani, A. Sorrentino, V. Speranza, G. Titomanlio, Rheol Acta , 2004, 43: 109.
5.R. Y. Chang and W. H. Yang, International Journalfor Numerical Methods in Fluids, 2001, 37: 125.
6.G. S. Layser, A. S. Cassebeer, and John P. Coulter,ANTEC Proceeding, 2007:2533.
7.P. J. Wang and H. E. Lai, ANTEC Proceeding,2007:2494. ■
